Norma española UNE 1-032-82. ISO 128.
A veces la representación en sistema diédrico en el que se trazan las vistas con un trazado de líneas ocultas dificultan la comprensión del dibujo por lo que es necesario aplicar cortes, secciones, roturas, en el mismo; éstos son elementos convencionales imaginarios que tratan de penetrar en el interior del cuerpo y mostrar de esta manera los detalles que encierran. Gracias a este artificio se eliminan las líneas ocultas discontinuas y en otros casos el número de proyecciones a representar.
Un corte es un recurso para separar de forma imaginaria un detalle de una pieza de manera que podamos ver el interior de la misma. Para hacer el corte se utiliza un plano imaginario que divide la pieza en dos partes, una, la que está delante del plano de corte y otra la que está detrás, la parte de atrás es la que se representa en el corte, perpendicular a dicho plano.
Por convención se establece que el corte sirve para ver la parte interior de la pieza, ello se consigue retirando siempre la parte de la pieza que está delante del plano que corta a la misma. A continuación se proyecta perpendicularmente al plano de proyección lo que queda detrás del plano de corte. El corte sólo afecta a la proyección donde viene representado y nunca a otras vistas, ello quiere decir que si en el alzado aparece la figura cortada, en la planta aparece completa.
Por convenio se ha establecido que el trozo de la pieza que aparece cortado no presenta líneas ocultas, esto quiere decir que las líneas que están detrás de él objeto cortado no se representan, pues interferirían en el rayado a 45° con el que se representa el corte.
La norma UNE 1032-74 diferencia entre sección y cortes, haciendo referencia a la primera como la parte cortada del objeto, mientras que el corte representa la sección más la parte del objeto que está detrás del plano secante.
Tenemos entonces que lo único que aparece rayado en el corte es la sección, mientras que en el corte aparece proyectada la sección más el resto de las líneas. Si cortamos una pieza por un plano y lo imaginamos de cristal y separamos la pieza anterior, lo que queda detrás del cristal sería exactamente lo que se vería en el corte: la sección más el resto de las líneas.
En los cortes totales el plano secante corta a la pieza en su totalidad longitudinalmente. En el corte del cuadrante, el plano es como si cortara a la pieza en dos direcciones ortogonales, sacando un cuarto de la misma y representando en un alzado la mitad de la pieza cortada. En un corte girado se utilizan como planos secantes dos planos no paralelos, girando uno de ellos hasta hacerlo coincidir con el otro en un plano de proyección paralelo. Los cortes de detalle o auxiliares se aplican a pequeños detalles del objeto. Los cortes parciales o locales corresponden a pequeñas porciones de la pieza, su contorno es irregular, como si se hubiera arrancado un trozo de la misma para ver el interior.
Las secciones y/o cortes transversales o giradas se hacen mediante un plano secante perpendicular al eje longitudinal de la pieza y se giran a continuación 90° para hacer coincidir la sección con el plano de proyección. Si para la comprensión del objeto hay que hacer demasiadas secciones transversales, se desplazan en la dirección del corte, mostrando una a continuación de la otra, son las secciones llamadas desplazadas.
Las roturas se utilizan para economizar espacio en el dibujo, se hacen en elementos largos como puede ser la representación de una farola.
La línea debe ser gruesa y en contornos vistos o aristas vistas de la pieza.
La línea debe ser fina recta o curva en líneas vistas ficticias y líneas de cota, en líneas de proyección, de referencia y en rayados. En contornos de secciones abatidas y en ejes cortos
La línea debe ser fina y hecha a mano alzada en los límites de vistas o en los cortes parciales o interrumpidos.
La línea debe ser fina llena y con zigzag en cortes interrumpidos.
La línea debe ser gruesa y con trazos (discontinua) en contornos ocultos que representan aristas ocultas.
La línea debe ser fina intercalando trozos y puntos en ejes de revolución, en las trazas de los planos de simetría y en trayectorias.
La línea debe ser fina con trazos y puntos intercalados y gruesa en los extremos en los cambios de dirección cuando se representan las trazas de los planos de corte imaginarios.
La línea debe ser gruesa intercalando trazos y puntos para indicar superficies y líneas con especificaciones particulares.
La línea debe ser fina de trazos continuos intercalando 2 puntos entre cada trozo, en el contorno de piezas adyacentes, en posiciones intermedias y extremos de piezas móviles, en las líneas que representan centros de gravedad, en contornos iniciales antes de la construcción de la pieza, en las partes situadas delante de un plano de corte.
La relación entre los anchos de las líneas gruesas y finas no debe ser nunca inferior a dos unidades. La línea se elegirá en función del tipo del dibujo y estará comprendida entre 0,18 y 2 mm. Siempre debe tener la misma anchura la línea correspondiente a las distintas vistas de una pieza. Cuando dos líneas en el dibujo son coincidentes, la prioridad se le dará a los contornos o aristas vistas, luego a los contornos con aristas ocultas, a continuación a las trazas de los planos de corte, a continuación a los ejes de revolución y trazas de los planos de simetría, después a las líneas correspondientes a los centros de gravedad y por último a las líneas de proyección.
La línea de referencia: se utiliza para indicar un elemento de un contorno, o línea de cota, referencia a tipo de rosca, etc. La línea de referencia termina en un punto si su extremo está en el interior del objeto representado, terminan en una flecha si concluye en el contorno del objeto y no llevan ni punto ni flecha su extremo, si concluyen en una línea de cota.
Traza del plano de corte
El plano de corte se representa por una línea mixta formada por trazos de distinto grosor alternando siempre uno mayor y otro menor. A esta línea mixta que representa el lugar por donde pasa el plano de corte se le llama traza y lleva en sus extremos dos segmentos delineados con mayor grosor y sobre ellos dos flechas ortogonales a la misma en la dirección y sentido en el cual se aplica el corte, así como las letras que lo definen.
Si al cortar una pieza el plano de corte coincide con una de las caras, ésta no aparece seccionada, por lo que no se representa con el rayado correspondiente al corte.
La proyección sobre la cual se aplica el plano de corte es aquella paralela al plano de corte, nunca al resto de las vistas.
Las proyecciones auxiliares se ajustan a los cortes de las secciones, pero involucran sólo a un detalle de la misma.
Para representar la superficie que ha sido cortada o seccionada de forma imaginaria se emplea un rayado. Este ha de hacerse con un conjunto de líneas finas paralelas equidistantes que forman 45° respecto a la horizontal.
El rayado representa además tanto el color del material como el material mismo de la pieza. Por ejemplo, la fundición se expresa mediante un rayado equidistante de líneas finas, el acero intercala tres líneas juntas, a continuación un hueco, otras tres líneas juntas y así sucesivamente. El bronce dibuja dos líneas juntas, hueco, una línea discontinua, otro hueco y dos líneas juntas y así sucesivamente. El zinc dibuja una línea continua y dos discontinuas otra continua y dos discontinuas y así sucesivamente. El aluminio y las aleaciones ligeras se representan con una línea fina continua y tres discontinuas, otra fina y tres discontinuas, etc.
El rayado también hace referencia al color, por
ejemplo el gris se representa con líneas finas continuas equidistantes, el morado con dos líneas, a continuación un hueco y luego otros dos líneas y así sucesivamente. El anaranjado se representa una línea continua, otra discontinua, una continua, otra discontinua y así sucesivamente. El verde claro se representa en las dos direcciones a 45° dejando ver como resultado rectángulos.
Hoy en día ya no se hace uso apenas de estos elementos para representar colores o materiales, simplemente se incorporan estos datos en el cajetín, especificando el material exacto y su referencia de tipo técnica, comercial, etcétera.
El rayado de la sección debe ser muy delgado respecto a las líneas del contorno de la pieza, deben tener una inclinación de 45° respecto a la línea horizontal, excepto si la pieza tiene sus contornos a 45°, en este caso en el rayado se varían la dirección de las líneas mostrándolas horizontales. Otras veces las líneas van a 45° respecto a los ejes de simetría de una pieza.
Cuando el corte está producido sobre distintas partes de una misma pieza deben llevar idéntico rayado. El intervalo o distancia entre las líneas del rayado es relativo a las dimensiones del dibujo.
Las líneas del rayado correspondiente a un corte deben terminar exactamente en el contorno de la arista seccionada. Cuando las superficies que aparecen seccionadas son muy delgadas, en vez de dibujar un rayado sobre las mismas se representan en color obscuro como puede ser el negro. Si la superficie cortada es muy grande y no tiene detalles interiores es suficiente el rayado de una zona contigua al contorno con una anchura uniforme.
Si el plano de corte se efectúa sobre dos piezas adyacentes, las direcciones del rayado son opuestas. Cuando el plano de corte intercepta a tres o más piezas concurrentes, para que no coincidan dos direcciones, las líneas equidistantes de una de ellas se separan más o menos, para diferenciarlas de las otras.
Cuando una cota pasa por encima del rayado de la pieza, éste debe ser interrumpido dejando un hueco para que se pueda ver claramente el valor de la cota.
1- Los cortes totales:
- Pueden ser por un solo plano: plano de corte coincidente con el de simetría de la pieza (no se indica el plano de corte porque es evidente) o no coincidente (o no tiene simetría o el corte se hace por otro plano distinto). El plano del corte es paralelo al plano de proyección.
- Auxiliar, el plano de corte no es paralelo al plano de proyección, es una vista auxiliar en la que se incorpora un corte.
- Con giro, representa la pieza cortada por dos planos distintos, de manera que uno gira respecto a la intersección de ambos planos, hasta coincidir con él en la proyección. Del giro se desprende que la nueva vista tiene una longitud mayor que la otra vista de la pieza, y que sus elementos no están alineados en las dos proyecciones. Se utiliza especialmente en elementos en las que se quieren ver agujeros, radios, volantes, nervios, etc.
- Corte con planos paralelos. Son planos colocados de forma paralela que interceptan a los elementos de los que se quiere obtener la información. Sirve para detalles con planos de simetría paralelos, en la planta de la figura se indica la trayectoria de los cortes, o sea sus trazas y en el alzado se proyecta como si el corte lo hubiera generado un solo plano de ahí que no debe aparecer en el alzado la línea de intersección del cambio de dirección que marcan los distintos planos. Si facilitan más la comprensión de los distintos detalles del objeto se pueden representar los agujeros cortados a la mitad, por ser formas simétricas.
2- Corte de cuadrante o semicorte. Suele utilizarse en piezas huecas simétricas y cuerpos de revolución en el que queda claro cómo es la pieza eliminando un cuarto de la misma. De esta forma en el alzado aparece la mitad de la pieza cortada y la otra mitad el exterior de la pieza.
Como también es evidente el corte por un meridiano, éste no se indica en la planta, en este corte tampoco se representa la línea que separa la parte cortada de la parte completa, por ser un corte imaginario. Como ya se dejó indicado tampoco se hace referencia a las líneas que están detrás del objeto que se representan mediante líneas discontinuas, éstas nunca deben aparecer.
Según la norma DIN 6, los medios cortes de eje vertical se dispondrán a la derecha de este, mientras que para el eje horizontal se dispondrán por debajo del eje.
3-Corte parcial. Si el hueco de una pieza ocupa un pequeño espacio de
Nunca podrá coincidir la línea hecha a mano alzada con una línea o arista de la pieza. Igual que en otros cortes, cuando es evidente a que detalle se hace referencia en el corte no se indica la traza del plano de corte.
4-Corte de detalle. En este corte se aísla un detalle de la pieza ya que no interesa mostrar el resto. Por oposición al corte parcial no aparece dentro de la figura y por tanto no se separa del resto de la figura por una línea irregular, sino que el final de este corte aparece en una línea recta invisible, siempre perpendicular a las aristas de la pieza. En el corte de detalle siempre se debe indicar la trayectoria seguida por el corte, como se viene haciendo en todos los cortes, mediante una línea de trazo, con sus extremos gruesos y flechas para indicar la dirección y sentido de la observación del detalle, haciendo referencia a las letras sobre todo si hay varios cortes.
Elementos mecánicos: los elementos mecánicos macizos como tornillos, pasadores, chavetas, roblones, ejes, bulones, rótulas, etc., nunca se cortan en el sentido longitudinal, en el sentido de su eje geométrico, sólo se hace cuando el corte es transversal. Ello es debido a que el corte no aporta información al indicar detalles del interior de un tornillo o de una chaveta por ser macizos.
Cálculo de cortes:
http://sistema-diedrico.blogspot.com/2010/11/secciones.html
VÍDEO SOBRE CÁLCULO DE CORTES
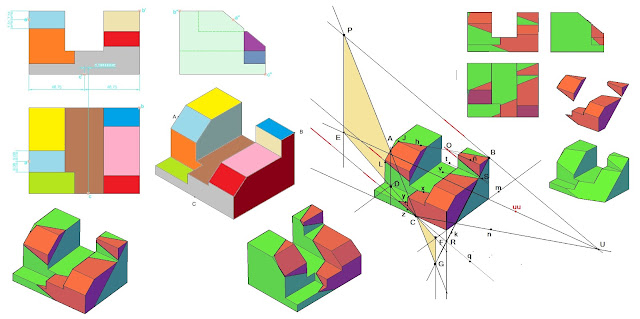
Si un plano corta a una pieza que tiene caras paralelas, las líneas de intersección del plano de corte con las caras paralelas son paralelas. En la pieza observamos que las caras paralelas del prisma paralelepípedo, al ser cortadas por un plano resultan paralelas sus líneas de intersección: a es paralela a b, c es paralela a d y e es paralela a f.
VÍDEO SOBRE CÁLCULO DE CORTES
Si un plano corta a una pieza que tiene caras paralelas, las líneas de intersección del plano de corte con las caras paralelas son paralelas. En la pieza observamos que las caras paralelas del prisma paralelepípedo, al ser cortadas por un plano resultan paralelas sus líneas de intersección: a es paralela a b, c es paralela a d y e es paralela a f.
Para calcular el corte de un plano determinado por tres puntos ABC, cuando ambos estaban situados sobre un mismo plano como es el caso de los puntos AB y BC, unimos ambos puntos mediante un segmento, este segmento de dirección número uno en el corte es por tanto la línea de intersección del plano cortante que pasa por ABC con la pieza sobre esa cara. En la figura los puntos AB están sobre una cara, hacemos por tanto la recta que pasa por ellos y la prolongamos hasta que corte a la prolongación de la arista h obteniendo de esta forma el punto M que unido con el punto de la otra cara C conseguimos la tercera dirección de la línea de sección. La segunda dirección resulta de unir mediante un segmento los puntos BC.
Si un plano de corte afecta a dos caras adyacentes, al prolongar las dos líneas de corte generadas por ese plano, obtenemos un punto P que siempre está sobre la intersección i de ambas caras. En la figura el punto P de intersección de las dos líneas de sección incide sobre la arista o prolongación de la arista i en este caso. Ello es debido a que un plano ABC (En este caso el de corte) corta a una recta i siempre en un punto P, pues si la cortara en dos, ésta recta estaría contenida en el plano ya que dos puntos determinan una recta.
El plano de corte intercepta al plano del suelo donde se apoya la pieza en una recta que llamamos traza, representada en el dibujo mediante una recta de color azul por los puntos PC.
Si prolongamos una línea de corte f de la pieza y su proyección m sobre el plano del suelo obtenemos siempre un punto P de intersección de ambas rectas que está sobre la traza PC del plano de corte.
Para calcular el corte que produce el plano ABC sobre la pieza, dibujamos las proyecciones ortogonales A’ B’ de los puntos AB sobre el plano en el que se apoya la pieza. Tomamos ambos puntos y los unimos mediante una recta que corta a la recta AB en el punto K. Como tenemos que éste punto pertenece al plano de corte por estar sobre la recta AB y teniendo además C del plano de corte sobre el suelo, la traza del plano de corte incide en los puntos KC. Tenemos así la dirección d1 que corta a otra arista de la pieza en el punto F, si unimos este punto con B es otra línea de sección por estar en la misma cara, al prolongar esta recta y la arista de la pieza s obtenemos un punto P de intersección que unido al punto A define la segunda dirección d2 del plano de corte. Para obtener la tercera dirección d3 podemos hacer exactamente lo mismo, prolongamos d2 hasta que corte a la arista t en el punto H, uniendo éste con C obtenemos la tercera dirección d3.
Para calcular el corte en la pieza que define el plano determinado por ABC, obtenemos las proyecciones A’ B’ C de esos puntos sobre el plano en el que se apoya la pieza. Al prolongar la recta AB tenemos que se corta con su proyección A’B’ en el punto P, (fuera del dibujo). Unimos P con C y ya tenemos la línea de corte MC del plano sobre la base de la figura. Si prolongamos otra arista de la base, por ejemplo la que pasa por el punto A’, observamos que corta a la recta MC en O. La recta que definen los puntos OA, determina la dirección CZ.
Para calcular el corte que produce el plano definido por los tres puntos ABC, unimos el punto C con B obteniendo la primera línea n de sección. Como este plano es paralelo al plano anterior de la pieza y A está en la en la prolongación de esa cara y como planos paralelos producen secciones paralelas, hacemos por A una recta paralela hasta que corte a la pieza según la línea PA. La línea PB corta a la pieza según la dirección m. Como planos paralelos producen secciones paralelas, obtenemos de inmediato las dos líneas de sección s o. Donde la recta o corta a la arista de la pieza hacemos una recta paralela t a la recta n. Las dos rectas m n cortan a las aristas de la pieza generando como sección la recta v, esta recta v será paralela a la que está en la parte posterior de la pieza, allí donde concluyen las dos líneas de sección t s, por ser planos paralelos.
Tenemos que calcular el corte que produce el plano ABC. Unimos los puntos AB y tenemos la dirección de corte sobre un plano horizontal, dirección que pasamos por C, obteniendo de esta forma la recta r, que corta al plano vertical que pasa por el punto A que en P. Como ambos puntos están en un mismo plano al prolongar los cortan a la arista anterior de ese prisma en el punto T, y unido con B defiende la otra dirección de corte de la pieza. De esta forma tenemos la dirección Z y S que son paralelas a la dirección BT.
Para calcular la sección que produce el plano ABC sobre la pieza, unimos los tres puntos obteniendo un triángulo que corta a dos caras de la pieza obteniendo de esta forma dos direcciones de la sección, la que corresponde a la línea AB y la que corresponde a la línea BC. Al construir la recta que pasa por los puntos AC tenemos la línea de corte correspondiente a los planos horizontales. La recta BC corta a la cara en P, haciendo por éste una recta paralela a la recta AB obtenemos F en la intersección con la prolongación de la arista superior de esa cara. Por F trazamos una recta paralela a la recta AC. De esta manera obtenemos también en la cara superior la recta d, paralela a la recta AC. Donde la recta d corta a la arista de la pieza bajamos otra recta paralela a BC y obtenemos la recta e. Donde esta recta corta al plano horizontal, hacemos otras recta paralela a la recta AC obteniendo el punto E en la prolongación de la arista de la pieza, por éste hacemos otra recta paralela a la recta BC, y obtenemos las recta u y así sucesivamente. AC es la traza del plano de corte, o línea de intersección del plano de corte con el plano en el que se apoya la pieza. Si prolongamos una arista x de la base de la pieza hasta que corta a la traza en y, a continuación por este punto de corte hacemos una paralela z a la recta BC, obtenemos otra recta de la sección, pues planos paralelos producen secciones paralelas. El mismo procedimiento nos sirve para construir la recta de corte TC, prolongamos m hasta que corta a la traza del plano AC y unimos este punto de corte C con el de intersección de la recta z con la pieza.
Para calcular el corte que produce el plano ABC en la pieza, mostrada en dos puntos de vista diferentes, unimos los tres puntos entre sí obteniendo en la intersección de la prolongación de estas rectas y en la prolongación de sus proyecciones A’B’C’ la traza del plano de corte de la pieza.
Para obtener la recta de corte v trazamos la traza m de ese plano vertical, por el punto de corte de esta recta con la recta C’B’ hacemos una vertical f que corta a la recta CB en el punto P. La intersección de la recta m con la traza del plano la unimos con P obteniendo la recta v, dirección de la sección sobre ese plano vertical y de los planos paralelos a él. La recta w la podemos construir por el mismo procedimiento, prolongando la arista de la base s hasta que corta a la traza del plano de corte y luego uniendo este punto de intersección con L.
Por un lado tenemos la recta AB y su proyección A’B’ que se cortan sobre la traza del plano, si tomamos otro punto de la traza por el que hacemos dos rectas n j que inciden en ambos puntos A A’ obtenemos en el extremo superior de la intersección i con el plano vertical que pasa por gB un punto que unido a B corta a la pieza en un punto F. Como la recta H es paralela a la recta v por ser planos paralelos, el punto donde concluye ésta lo unimos con F obteniendo la recta D. la intersección de la recta t con la arista vertical de la pieza determina el punto K por el que hacemos una recta paralela a la recta W, de esta forma tenemos la recta x. Los planos paralelos esta recta determinan también secciones paralelas a ella y los planos horizontales de la pieza tienen por intersección con el plano de corte rectas paralelas a la traza del plano de corte.
Para calcular el corte de la pieza por el plano determinado por los puntos IWG, unimos IW por estar en la misma cara de la pieza, obteniendo de esta manera la primera línea o de sección.
El plano j de la cara superior de la pieza que contiene al punto R se prolonga hasta obtener su cota por Z sobre la cara anterior, ésta cota corta a la traza del plano en el punto K. Si unimos este punto con G, obtenemos la línea de corte a.
Por E, punto de corte de la recta o con el plano horizontal más alto de la pieza, hacemos una recta paralela b a la anterior, por ser un plano paralelo a j. Esta recta corta a la base de la pirámide en P, si lo unimos con W. tenemos s, la línea de corte sobre la cara de la pirámide. La recta v es paralela a o por ser planos paralelos, el extremo de s y v definen t.
Si por H hacemos una recta ñ paralela a o, obtenemos N en la intersección con la cuña de la figura. La línea NG es la correspondiente a la sección del plano sobre esa cara.
Dada la pieza de la izquierda, se trata de calcular el corte que produce el plano definido por los puntos ABC. La pieza aparece cortada y separada en dos fragmentos en el centro y a la derecha del dibujo, a la derecha se han dibujado las líneas de la sección correspondientes a las tres direcciones d1 d2 d3 de los tres planos de la figura, que son seccionados por el plano ABC.
La localización de los puntos que definen el plano de corte está determinada por rectas paralelas a los ejes cartesianos, el punto B está sobre el suelo y la proyección ortogonal sobre la arista de la base es el punto Pb. El punto A está por debajo del suelo y si hacemos una recta perpendicular a la arista de la base más cercana tenemos localizado el mismo mediante el punto Pa. De igual forma el punto C está por encima de la cara superior de la pieza y si hacemos una recta perpendicular a la arista más cercana de la misma tenemos como recta de intersección con la arista el punto Pc.
Para calcular el corte unimos los puntos AC y dibujamos su proyección A’C’ sobre el plano del suelo en el que se apoya la pieza, la intersección de ambas rectas nos determinan el punto V, que unido con B define la traza del plano de corte. Tenemos por tanto la línea de sección d3 correspondiente a los planos horizontales.
Para determinar el punto por donde pasa esta dirección de corte, hacemos por U una recta f paralela a A’V Y donde corta a la recta AC obtenemos el punto P por el que hacemos una recta n paralela a la traza del plano VB, con lo que tenemos ya la dirección de la línea de sección sobre el plano superior de la pieza.
Si tomamos un punto cualquiera de la traza del plano de corte, por ejemplo el punto O y trazamos por él dos líneas paralelas g h a las rectas AC y f respectivamente, tenemos que la línea horizontal corta a la arista de la pieza en el punto D, por el que hacemos una vertical determinando en la intersección con la recta g el punto Z, la recta ZV es por tanto la dirección de la línea de sección correspondiente a este plano y a los planos paralelos al mismo.
En consecuencia si prolongamos la recta n hasta que corte a la prolongación de la arista k tenemos un punto de intersección T por el que hacemos una recta r paralela a la recta ZI, con lo cual tenemos ya determinada la última dirección de la sección d2 del plano de corte.
Si prolongamos ZV hasta que corte a w en el punto m, uniendo los puntos mq tenemos la dirección de la línea de corte d1.
-------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------
-------------------------------------------------------------------------------------------------
En este dibujo podemos ver un corte con planos paralelos y definido por los puntos AA. Siguiendo el sentido de las flechas vemos que el corte produce en la figura tres secciones. Como no se representa la parte de atrás de la pieza, sólo la intersección del plano de corte con la pieza, tenemos que es una sección.
En este dibujo tenemos el mismo corte que en la figura anterior, pero en la proyección aparecen añadidas las líneas del contorno de la pieza, por lo que tenemos que lo que se muestra aquí es un corte con planos paralelos.
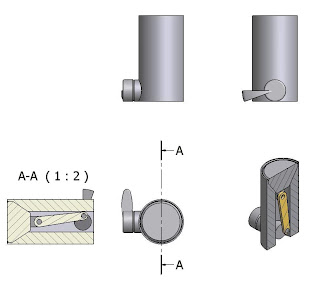
En la figura podemos ver un elemento mecánico con dos tornillos cortados en sección longitudinal, por eso no aparecen con el rayado correspondiente a la sección. Vemos no obstante un corte transversal de un pasador que sí aparece con el rayado ya que es un corte transversal, si fuera longitudinal no aparecería rayado. El rayado de esta pieza no es a 45° porque si lo fuera se interpretaría que sería parte de la misma pieza que está a la izquierda y cuyo rayado es también a 45° pero en el otro sentido, a no ser que se hubieran juntado o separado más las líneas, opción más adecuada a la normativa.
En el dibujo podemos ver un corte quebrado con la traza del plano de corte con dos planos paralelos y uno ortogonal a los mismos. Como podemos ver en la perspectiva, si quitamos todo lo que queda delante del plano de corte, nos queda ese trozo de la pieza en el que la sección aparece con un rayado a 45°. En la planta se define la traza del plano de corte y se proyecta siguiendo la dirección y sentido de las flechas haciendo un giro de 90° de lo que queda en este caso a la derecha del plano de corte.
Observamos el dibujo anterior en el que se representa la curvatura de las líneas de intersección de los dos cilindros. Si bien intuitivamente es más fácil de comprender el detalle de la pieza, a la hora de dibujar resulta más engorroso.
En la figura podemos observar las tres proyecciones diédricas de una pieza, planta, alzado y perfil. Para facilitar una mejor inteligibilidad de la pieza, se ha hecho una sección del perfil de manera que la nueva proyección del corte aparece a la derecha de éste y tiene como contorno una figura igual al alzado.
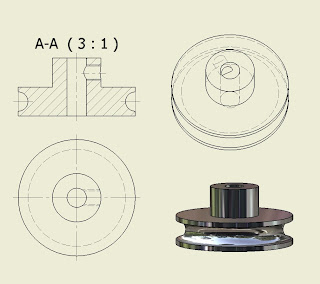
En la figura podemos observar un corte total de la pieza que muestra proyectado y abatido 90° la sección del mismo por un plano meridiano. Por regla general los cortes que pasan por la mitad del objeto porque son secciones meridianas, no suelen indicar la traza de corte del plano, no obstante como la sección no da mucha información de la pieza en este caso se ha resuelto dejar indicada la traza del plano de corte. Como el plano de corte atraviesa tres partes distintas de la pieza, éstas llevan distinto rayado, dos rayados a 45° y otro en el que se ha variado el ángulo. Si fuéramos estrictos con la norma, en el tercer rayado de la pieza se le exigiría que fuera también a 45° pero con una equidistancia entre las líneas mayor o menor que la otra superficie cortada a 45° y cuyo rayado coincidiría con ésta.
En la figura podemos observar que el dibujo queda más claro mostrando un corte del mismo, en este caso sí que se podría prescindir totalmente de la traza del plano de corte que aparece en la planta de la figura. La figura aparece en planta, alzado y perfil y muestra una perspectiva axonométrica en la que se puede observar el interior gracias al corte que se ha practicado.
En el dibujo podemos observar algo que no se debe hacer: en la figura en planta podemos observar la aplicación de un corte meridiano total de la figura que, al proyectarlo hacia abajo muestra un perfil igual al alzado pero deja mostrar el 50% del interior de la figura. Como sabemos el corte es un artificio imaginario, para eso se muestra el rayado, si la pieza fuera cortada directamente no llevaría el rayado y aparecería tal y como es. En este caso, en el corte imaginario que muestra el 50% de la pieza, se hace otro corte definido por la traza. Si hacemos un corte de otro corte estamos representando una parte del objeto que no es real, por lo que no debemos hacer un corte a partir de otro.
En la figura observamos un cilindro en planta y alzado, un corte en diagonal produce una sección elíptica. Con la elipse de color rojo se ha señalado que el extremo de la traza del corte coincide con el vértice superior derecho de la figura. La traza del plano de corte nunca debe coincidir con la figura, sino que debe sobresalir de ésta para que quede más claro el dibujo, por lo que tenemos que esta traza del plano de corte está mal representada.
En esta figura se puede ver claramente el interés de un corte. La figura está formada por un elemento con varios cilindros a los que les falta algunas partes, si en el corte no apareciera perfectamente el rayado que define el perfil de la figura, podríamos confundir el corte de la pieza con las líneas reales de la pieza. El rayado del corte define y aclara perfectamente lo que es parte de la figura y lo que es el interior que define el corte. Podemos observar en la figura que el plano de corte es tangente a una de las caras de la misma, la norma dice que si el plano es tangente no se debe marcar el rayado del mismo (ya que no lo corta, sólo lo toca), salvo excepciones como ésta en las cuales clarifica más el dibujo.
En el dibujo aparece una pieza en planta, alzado y perfil, la pieza está acotada y muestra en el alzado un corte que proyectado a la izquierda define un perfil idéntico al perfil derecho de la pieza. Normalmente con la sección del perfil hubiera bastado, por lo que podríamos prescindir del perfil derecho de la figura, no obstante se muestra este perfil para que se vea claramente la diferencia entre una proyección mostrada en corte y otra proyección definida sólo por las líneas continuas (las que quedan delante del “observador”).
Podemos observar en el dibujo una superficie de revolución que ha sido atravesada por un prisma paralelepípedo. Aunque también muestra un exceso de proyecciones dada la sencillez de la figura, podemos determinar si sería más claro representar por ejemplo el perfil de la figura o la sección de la misma. Quizás la solución más óptima sería representar un corte de semicuadrante, un corte en el que en el alzado apareciera cortada la figura al 50%, la mitad izquierda con el rayado apreciándose al corte la pieza por el interior, y a la derecha del exterior de la pieza con todas las líneas continuas y sin dejar ver las líneas que aparecerían detrás de la pieza.
chévere
ResponderEliminar